Overview
This section consists of various projects, with a focus on technology applications, which demonstrate the advanced functionality of Meep and MPB. Refer to their homepages for an introduction to each software package including descriptions of core features and user interface as well as tutorials demonstrating basic functionality. Each project consists of a simulation script, a shell script to run the simulation, and Python post-processing routines for visualizing the output. Additional routines for Matlab/Octave are also provided. A version of this page is available for the Python user interface.- Meep Project #1 — Light-Extraction Efficiency of Organic Light Emitting Diodes (OLEDs)
- MPB Project #1 — Modes of Silicon on Insulator (SOI) Strip Waveguides
- Meep Project #2 — Optimizing Far-Field Radiated Power of SOI Bragg Grating Outcouplers
- MPB Project #2 — Band Gap of Photonic-Crystal Nanobeam Waveguide
- Meep Project #3 — Resonant Modes of a Photonic-Crystal Nanobeam Cavity
- Meep Project #4 — Near-Infrared Absorption Spectra of CMOS Image Sensors
- Meep Project #5 — Thermal Radiation Spectra of Plasmonic Metamaterials
- Meep Project #6 — Bidirectional Scattering Distribution Function (BSDF) of Asymmetric Gratings
Meep Project #1 — Light-Extraction Efficiency of Organic Light Emitting Diodes (OLEDs)
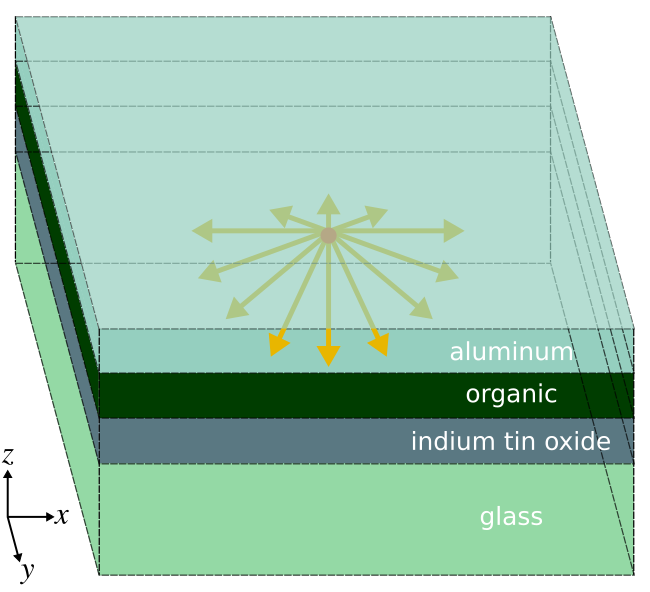
Organic light-emitting diodes (OLEDs) are being increasingly used in display applications involving mobile devices and televisions due to their higher contrast ratios, color uniformity, and wider viewing angle than liquid-crystal displays. One of the main limitations of OLED energy efficiency is the low light extraction from the device. In this example, we use Meep to compute the light-extraction efficiency of an OLED. This is based on results published in Applied Physics Letters, Vol. 106, No. 041111, 2015 (pdf). US Patent 9761842, related to this work, has been licensed by Universal Display Corporation (NASDAQ: OLED).A typical device structure for a bottom-emitting OLED is shown below. The device consists of a stack of four planar layers. The organic (ORG) layer is deposited on an indium tin oxide (ITO) coated glass substrate with an aluminum (Al) cathode layer on top. Electrons are injected into the organic layer from the Al cathode and holes from the ITO anode. These charge carriers form bound states called excitons which spontaneously recombine to emit photons. Light is extracted from the device through the transparent glass substrate. Some of the light, however, remains trapped within the device as (1) waveguide modes in the high-index ORG/ITO layers and (2) surface-plasmon polaritons (SPP) at the Al/ORG interface. These losses significantly reduce the external quantum efficiency (EQE) of OLEDs. We compute the fraction of the total power in each of these three device components for broadband emission from a white source spanning 400 to 800 nm. The results can be obtained using just one finite-difference time-domain (FDTD) simulation.
There are three key features involved in developing an accurate model. (1) Material Properties: The complex refractive index over the entire broadband spectrum must be imported for each material. This requires fitting the material data to a sum of Drude-Lorentzian susceptibility terms. In this example, we treat the glass, ITO, and organic as lossless since their absorption coefficient is small. The refractive index of Al can be obtained from Applied Optics, Vol. 37, pp. 5271-83, 1998. (2) Recombining Excitons as Light Source: An ensemble of spontaneously-recombining excitons produces incoherent emission. This can be modeled using a collection of point-dipole sources with random phase positioned within the organic layer. Given the stochastic nature of the sources, the results must be averaged using Monte-Carlo sampling. The number of samples must be large enough to ensure that the variance of the computed quantities is sufficiently small. (3) Flux Monitors: The total power separated into the three device components is computed using flux monitors. The size and position of these monitors must be chosen correctly to fully capture the relevant fields.
(set-param! resolution 100) ; pixels/μm
We specify the frequency bounds of the Gaussian pulse using its minimum and maximum wavelengths in vacuum.
(define-param lambda-min 0.4) ; minimum source wavelength
(define-param lambda-max 0.8) ; maximum source wavelength
(define fmin (/ lambda-max)) ; minimum source frequency
(define fmax (/ lambda-min)) ; maximum source frequency
(define fcen (* 0.5 (+ fmin fmax))) ; source frequency center
(define df (- fmax fmin)) ; source frequency width
The thickness of each layer is a parameter. This is useful if we want to optimize the design. We use typical values for OLEDs. The length of the absorbing layer should be at least half the largest wavelength in the simulation to ensure negligible reflections. This is because incident waves are absorbed twice through a round-trip reflection from the hard-wall boundaries of the computational cell.
(define-param tABS lambda-max) ; absorber/PML thickness
(define-param tGLS 1) ; glass thickness
(define-param tITO 0.1) ; indium tin oxide thickness
(define-param tORG 0.1) ; organic thickness
(define-param tAl 0.1) ; aluminum thickness
; length of computational cell along Z
(define sz (+ tABS tGLS tITO tORG tAl))
Since this is a 3d simulation, we also need to specify the length of the computational cell in the transverse directions X and Y. This is the length of the high-index organic/ITO waveguide. We choose a value of several wavelengths. The choice of the waveguide length has a direct impact on the results.
; length of non-absorbing region of computational cell in X and Y
(define-param L 4)
(define sxy (+ L (* 2 tABS)))
(set! geometry-lattice (make lattice (size sxy sxy sz)))
Overlapping the lossy-metal aluminum with a perfectly-matched layer (PML) sometimes leads to field instabilities due to backward-wave SPPs. Meep provides an alternative absorber which tends to be more stable. We use an absorber in the X and Y directions and a PML for the outgoing waves in the glass substrate. The metal cathode on top of the device either reflects or absorbs the incident light. No light is transmitted. Thus, we need a PML along just one side in the Z direction.
(set! pml-layers (list
(make absorber (thickness tABS) (direction X))
(make absorber (thickness tABS) (direction Y))
(make pml (thickness tABS) (direction Z) (side High))))
Next, we define the material properties and set up the geometry consisting of the four-layer stack. Aluminum (Al) is imported from Meep's materials library.
(define ORG (make medium (index 1.75)))
(define ITO (make medium (index 1.80)))
(define GLS (make medium (index 1.45)))
(set! geometry (list
(make block (material GLS) (size infinity infinity (+ tABS tGLS))
(center 0 0 (- (* 0.5 sz) (* 0.5 (+ tABS tGLS)))))
(make block (material ITO) (size infinity infinity tITO)
(center 0 0 (- (* 0.5 sz) tABS tGLS (* 0.5 tITO))))
(make block (material ORG) (size infinity infinity tORG)
(center 0 0 (- (* 0.5 sz) tABS tGLS tITO (* 0.5 tORG))))
(make block (material Al) (size infinity infinity tAl)
(center 0 0 (- (* 0.5 sz) tABS tGLS tITO tORG (* 0.5 tAl))))))
We use a set of point-dipole sources, each with random phase but fixed polarization, distributed along a line within the middle of the organic layer. The number of point sources is a parameter with a default of 10. The polarization of the source has an important effect on the results which we will investigate. Instead of using a random polarization, which would require multiple runs to obtain a statistical average, the sources can be separated into components which are parallel (directions X and Y) and perpendicular (Z) to the layers. Thus, we will need to do just two sets of simulations. These are averaged to obtain results for random polarization.
; random number generator: uniformly distributed in [-1,1]
(define random-num (lambda ()
(let ((time (gettimeofday)))
(set! *random-state* (seed->random-state (+ (car time) (cdr time)))))
(if (> (random:uniform) 0.5) (random:uniform) (* -1 (random:uniform)))))
(define-param perp-dipole? true)
(define src-cmpt (if perp-dipole? Ez Ex)) ; current source component
(define-param num-src 10) ; number of point sources
(set! sources
(map (lambda (cz)
(make source
(src (make gaussian-src (frequency fcen) (fwidth df)))
(component src-cmpt) (center 0 0 (- (* 0.5 sz) tABS tGLS tITO (* 0.4 tORG) (* 0.2 cz tORG)))
(amplitude (exp (* 0+2i pi (abs (random-num)))))))
(arith-sequence (/ num-src) (/ num-src) num-src)))
(set! force-complex-fields? true)
We can also exploit the two mirror symmetry planes of the sources and the structure in order to reduce the size of the computation by a factor four. The phase of the mirror symmetry planes depends on the polarization of the source. Three separate cases are necessary. Finally, since only the source and not the structure is being changed between runs, we can store the epsilon in the first run as an HDF5 file and load it back in during subsequent runs. This speeds up the calculation by forgoing subpixel smoothing which is time intensive. An input parameter load-structure? specifies whether to load the structure from file or save the geometry to file.
(if (= src-cmpt Ex)
(set! symmetries (list
(make mirror-sym (direction X) (phase -1))
(make mirror-sym (direction Y) (phase +1)))))
(if (= src-cmpt Ey)
(set! symmetries (list
(make mirror-sym (direction X) (phase +1))
(make mirror-sym (direction Y) (phase -1)))))
(if (= src-cmpt Ez)
(set! symmetries (list
(make mirror-sym (direction X) (phase +1))
(make mirror-sym (direction Y) (phase +1)))))
(define-param load-structure? false)
(if load-structure?
(begin
(set! geometry '())
(init-structure)
(meep-structure-load structure "oled-epsilon.h5")))
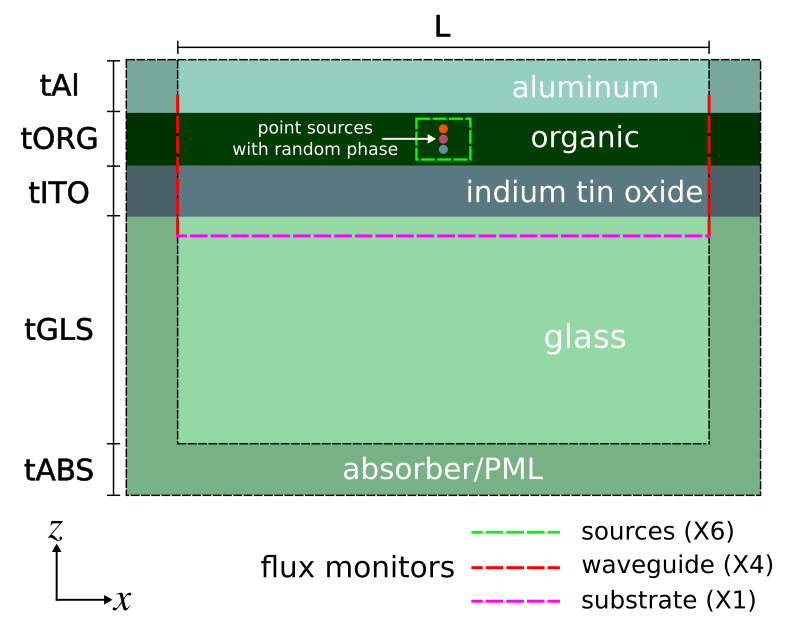
Three sets of flux monitors are required to capture the power in the sources, glass substrate, and high-index waveguide. We place a set of six flux planes along the sides of a box to enclose the sources. This is used to compute the total power in the device. These monitors must be placed entirely within the organic layer. One flux plane is required to compute the power in the glass substrate. Four flux planes are required to capture the total power of the modes in the high-index waveguide forming the organic/ITO layers. These modes are delocalized and extend slightly beyond these two layers. This requires the height of the flux planes to be larger than the combined thickness of the layers as shown in the figure above. Also, any component of the guided mode which extends into the aluminum will be absorbed due to screening effects of the charges in the metal. The longer the waveguide is made, the more these guided modes will be absorbed. This is why the length of the waveguide (L) should not be made so large that the waveguide component of the total power is zero.
; number of frequency bins for DFT fields
(define-param nfreq 50)
; surround source with a six-sided box of flux planes
(define srcbox-width 0.05)
(define srcbox-top (add-flux fcen df nfreq
(make flux-region (size srcbox-width srcbox-width 0) (direction Z)
(center 0 0 (- (* 0.5 sz) tABS tGLS)) (weight +1))))
(define srcbox-bot (add-flux fcen df nfreq
(make flux-region (size srcbox-width srcbox-width 0) (direction Z)
(center 0 0 (- (* 0.5 sz) tABS tGLS tITO (* 0.8 tORG))) (weight -1))))
(define srcbox-xp (add-flux fcen df nfreq
(make flux-region (size 0 srcbox-width (+ tITO (* 0.8 tORG))) (direction X)
(center (* 0.5 srcbox-width) 0 (- (* 0.5 sz) tABS tGLS (* 0.5 (+ tITO (* 0.8 tORG))))) (weight +1))))
(define srcbox-xm (add-flux fcen df nfreq
(make flux-region (size 0 srcbox-width (+ tITO (* 0.8 tORG))) (direction X)
(center (* -0.5 srcbox-width) 0 (- (* 0.5 sz) tABS tGLS (* 0.5 (+ tITO (* 0.8 tORG))))) (weight -1))))
(define srcbox-yp (add-flux fcen df nfreq
(make flux-region (size srcbox-width 0 (+ tITO (* 0.8 tORG))) (direction Y)
(center 0 (* 0.5 srcbox-width) (- (* 0.5 sz) tABS tGLS (* 0.5 (+ tITO (* 0.8 tORG))))) (weight +1))))
(define srcbox-ym (add-flux fcen df nfreq
(make flux-region (size srcbox-width 0 (+ tITO (* 0.8 tORG))) (direction Y)
(center 0 (* -0.5 srcbox-width) (- (* 0.5 sz) tABS tGLS (* 0.5 (+ tITO (* 0.8 tORG))))) (weight -1))))
; padding for flux box to capture extended waveguide mode
(define fluxbox-dpad 0.05)
; upward flux into glass substrate
(define glass-flux (add-flux fcen df nfreq
(make flux-region (size L L 0) (direction Z)
(center 0 0 (- (* 0.5 sz) tABS (- tGLS fluxbox-dpad))) (weight +1))))
; surround ORG/ITO waveguide with four-sided box of flux planes
; NOTE: waveguide mode extends partially into Al cathode and glass substrate
(define wvgbox-xp (add-flux fcen df nfreq
(make flux-region (size 0 L (+ fluxbox-dpad tITO tORG fluxbox-dpad)) (direction X)
(center (* 0.5 L) 0 (- (* 0.5 sz) tABS tGLS (* 0.5 (+ tITO tORG)))) (weight +1))))
(define wvgbox-xm (add-flux fcen df nfreq
(make flux-region (size 0 L (+ fluxbox-dpad tITO tORG fluxbox-dpad)) (direction X)
(center (* -0.5 L) 0 (- (* 0.5 sz) tABS tGLS (* 0.5 (+ tITO tORG)))) (weight -1))))
(define wvgbox-yp (add-flux fcen df nfreq
(make flux-region (size L 0 (+ fluxbox-dpad tITO tORG fluxbox-dpad)) (direction Y)
(center 0 (* 0.5 L) (- (* 0.5 sz) tABS tGLS (* 0.5 (+ tITO tORG)))) (weight +1))))
(define wvgbox-ym (add-flux fcen df nfreq
(make flux-region (size L 0 (+ fluxbox-dpad tITO tORG fluxbox-dpad)) (direction Y)
(center 0 (* -0.5 L) (- (* 0.5 sz) tABS tGLS (* 0.5 (+ tITO tORG)))) (weight -1))))
Finally, with the structure and sources set up, we run the simulation until the fields in the device have sufficiently decayed away. Afterwards, the flux data is written to standard output as a series of columns.
(run-sources+ (stop-when-fields-decayed 50 src-cmpt (vector3 0 0 (- (* 0.5 sz) tABS tGLS tITO (* 0.5 tORG))) 1e-8))
(if (not load-structure?) (meep-structure-dump structure "oled-epsilon.h5"))
(display-fluxes srcbox-top srcbox-bot srcbox-xp srcbox-xm srcbox-yp srcbox-ym glass-flux wvgbox-xp wvgbox-xm wvgbox-yp wvgbox-ym)
We use the following Bash script to launch a parallel Meep simulation using 20 processors.
#!/bin/bash
mpirun -np 20 meep L=$1 oled-ext-eff.ctl > oled-flux.out;
grep flux1: oled-flux.out |cut -d , -f2- > oled-flux.dat;
This script is executed from the shell terminal using a waveguide length (L) of 4.
chmod u+x run_oled.sh
nohup ./run_oled.sh 4 &> /dev/null &
This takes about 3 hours to run on an Intel Xeon 2.60 GHz machine. Once the simulation is complete, we plot its output using Octave/Matlab. The total power in each device component is the sum of the relevant columns of the output.
f = load('oled-flux.dat');
% total power emitted from sources
total_power = f(:,2)+f(:,3)+f(:,4)+f(:,5)+f(:,6)+f(:,7);
% total power in glass
glass_power = f(:,8);
% total power in waveguide mode
waveguide_power = f(:,9)+f(:,10)+f(:,11)+f(:,12);
if (length(find(f(:,2:12) < 0)) > 0)
disp(sprintf("warning: flux is negative"));
endif
% fraction of total power in each of three regions
glass = glass_power./total_power;
waveguide = waveguide_power./total_power;
aluminum = 1-glass-waveguide;
% wavelengths (um)
lambdas = 1./f(:,1);
if (sum(aluminum < 0) > 0)
disp(sprintf("warning: aluminum absorption is negative"));
endif
if (sum(aluminum > 1) > 0)
disp(sprintf("warning: aluminum absorption is larger than 1"));
endif
lambdas_linear = linspace(0.4,0.8,100).';
glass_linear = interp1(lambdas,glass,lambdas_linear,"spline","extrap");
waveguide_linear = interp1(lambdas,waveguide,lambdas_linear,"spline","extrap");
aluminum_linear = interp1(lambdas,aluminum,lambdas_linear,"spline","extrap");
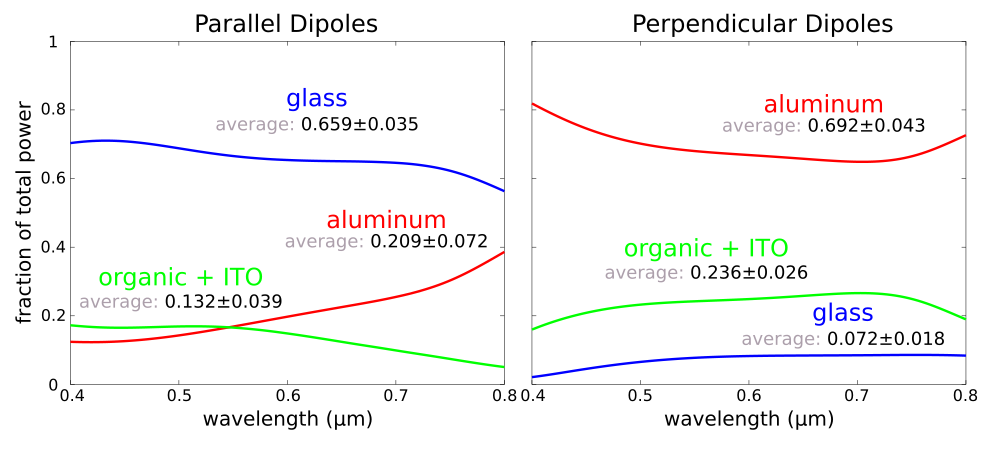
plot(lambdas_linear,glass_linear,'b-',lambdas_linear,aluminum_linear,'r-',lambdas_linear,waveguide_linear,'g-');
xlabel("wavelength (um)"); ylabel("fraction of total power");
legend("glass","aluminum","organic + ITO");
axis([0.4 0.8 0 1]);
disp("power in each region averaged over all wavelengths");
disp(sprintf("glass: %0.6f, %0.6f",mean(glass_linear),std(glass_linear,1)));
disp(sprintf("aluminum: %0.6f, %0.6f",mean(aluminum_linear),std(aluminum_linear,1)));
disp(sprintf("organic + ITO: %0.6f, %0.6f",mean(waveguide_linear),std(waveguide_linear,1)));
Files: Simulation Script, Shell Launch Script, Plot Results. [gzipped tarball]
MPB Project #1 — Modes of Silicon on Insulator (SOI) Strip Waveguides
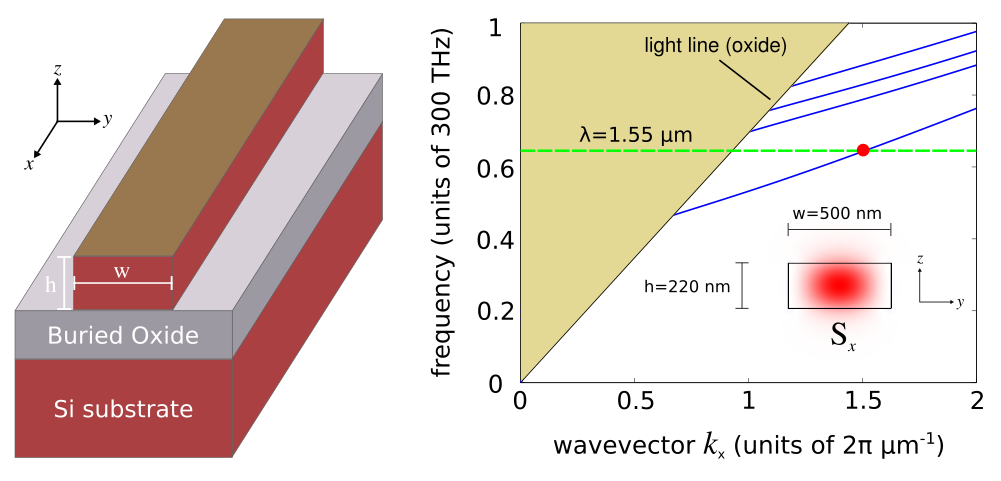
A key component of silicon photonic integrated circuits are waveguides. These devices are typically fabricated on silicon on insulator (SOI) wafers. Infrared light at 1.55 μm, the standard wavelength for telecommunications using silica fibers, is routed within the silicon using index guiding. We will use MPB to calculate the dispersion relation, also known as a band diagram, of these waveguide modes as shown in the right figure below. The focus is to design a waveguide which is single mode for the lowest band (i.e., the fundamental mode).The left figure shows the device structure. The silicon waveguide has a rectangular cross section with width w and height h. The buried oxide, typically silicon dioxide, is below the waveguide. A silicon substrate is beneath. No cladding is placed on top of the waveguide which is surrounded by air. The propagation axis is along X. This is the direction in which the waveguide is translationally invariant.
(set-param! resolution 64) ; pixels/μm
The width and height of the waveguide are design parameters. Most SOI wafers have a 220 nm thick silicon layer which is used as the default value for the height. The default width is 500 nm.
(define-param w 0.50) ; waveguide width
(define-param h 0.22) ; waveguide height
This is a 3d calculation based on a 2d computational cell in Y and Z. The size of the computational cell needs to be large enough such that the fields are negligible at the edge of the computational cell. This ensures that MPB's periodic boundaries do not affect the results. Since the guided mode is localized within the silicon, the fields outside are exponentially decaying. There is a tradeoff to increasing the size of the computational cell: the size of the calculation also increases.
(define-param sc-y 2) ; supercell width
(define-param sc-z 2) ; supercell height
(set! geometry-lattice (make lattice (size no-size sc-y sc-z)))
Next, we specify the material properties of silicon and silicon dioxide. Silicon is lossless at 1.55 μm which is an important feature for these kinds of applications. The large refractive index contrast with silicon dioxide also produces strong mode confinement. Typical values for the refractive indicies are used as default.
(define-param nSi 3.45)
(define-param nSiO2 1.45)
(define Si (make dielectric (index nSi)))
(define SiO2 (make dielectric (index nSiO2)))
Since the oxide layer in which the waveguide modes are exponentially decaying is several microns in thickness, the fields are negligible at the silicon substrate. Thus, the substrate can be omitted from the device geometry. The geometry consists of just two objects: (1) a rectangular silicon waveguide at the center of the computational cell and (2) a planar oxide layer which fills the bottom half.
(set! geometry (list
(make block (size infinity w h)
(center 0 0 0) (material Si))
(make block (size infinity infinity (* 0.5 (- sc-z h)))
(center 0 0 (* 0.25 (+ sc-z h))) (material SiO2))))
The first four bands will be computed even though the single-mode property can be determined from only the first and second bands. The range of propagation wavevectors over which to compute the bands needs to be sufficiently large to contain modes at 1.55 μm. Finding suitable values typically requires a bit of trial and error.
(set-param! num-bands 4)
(define-param num-k 20)
(define-param k-min 0.1)
(define-param k-max 2.0)
(set! k-points (interpolate num-k (list (vector3 k-min) (vector3 k-max))))
We can now call the run function to compute the bands. The parity information in the Y direction for each mode is also output. This will help us identify properties of the modes since the fundamental mode has even symmetry.
(run display-yparities)
After the bands have been computed, we identify the mode(s) at 1.55 μm. This involves an inverse calculation where given the mode frequency (in vacuum), we compute its wavevector using MPB's built-in find-k routine. The Poynting vector along X of the fields is also output as an HDF5 file.
(define-param f-mode (/ 1.55)) ; frequency corresponding to 1.55 um
(define-param band-min 1)
(define-param band-max 1)
(define-param kdir (vector3 1 0 0))
(define-param tol 1e-6)
(define-param kmag-guess (* f-mode nSi))
(define-param kmag-min (* f-mode 0.1))
(define-param kmag-max (* f-mode 4))
(find-k ODD-Y f-mode band-min band-max kdir tol
kmag-guess kmag-min kmag-max
output-poynting-x display-group-velocities)
This shell script is used to launch the simulation which takes a few seconds using a single Intel Xeon 2.60 GHz core. Afterwards, h5topng, part of the h5utils package, is used to generate a PNG image from the raw simulation data stored in the HDF5 file.
#!/bin/bash
mpb strip-wvg.ctl > strip-wvg-bands.out;
grep freqs: strip-wvg-bands.out |cut -d , -f3,7- |sed 1d > strip-wvg-bands.dat;
h5topng -o wvg_power.png -x 0 -d x.r -vZc bluered -C strip-wvg-epsilon.h5 strip-wvg-flux.v.k01.b01.x.yodd.h5;
Finally, we plot the results from the output and add the light line for the oxide.
f = dlmread("strip-wvg-bands.dat");
plot(f(:,1),f(:,2:end),'b-',f(:,1),f(:,1)/1.45,'k-');
xlabel("wavevector k_x (units of 2\pi \mum^{-1})");
ylabel("frequency (units of 300 THz)");
axis([0 2 0 1]);
This plot is shown in the right figure above. There is a single mode at 1.55 μm for the lowest band indicated with the dotted green line. The cutoff frequency of the second band lies above this mode frequency. The inset shows the Poynting vector along X (Sx). The antinode at the center of the waveguide verifies that this is the fundamental mode. This mode has a wavevector at 1.5192 μm-1 as calculated from the find-k routine.Files: Simulation Script, Shell Launch Script, Plot Results. [gzipped tarball]
Meep Project #2 — Optimizing Far-Field Radiated Power of SOI Bragg Grating Outcouplers
Coupling light into and out of silicon photonic integrated circuits is an important part of the overall device operation. For example, couplers are required when an external laser is used as the input light source or when the circuit signal must be transferred to an optical fiber for long-range transmission. This example involves designing a grating structure to outcouple light from an SOI strip waveguide and direct the beam into a given direction in the vacuum far field while minimizing losses due to reflection and scattering. We will use Meep to compute the far-field radiated power of the device and optimize the design by integrating Meep with NLopt, an open-source library for nonlinear optimization.The outcoupler design is based on Optics Express, Vol. 22, pp. 20652-62, 2014 which is a concentric Bragg grating with angled sides, shown in the figures below. The input port is an SOI strip waveguide which is connected to the Bragg grating.

The figure below shows the device cross section in the XY plane of the computational cell. There are two parameters used to design the Bragg grating outcoupler: periodicity a and length d. In this example, the number of grating periods and the side angle are constants (5° and 20°). The width w and height h of the waveguide are 500 nm and 220 nm, identical to the single-mode waveguide described in the previous section. An eigenmode source is placed at the left edge of the input port to excite the waveguide mode at 1.55 μm. The computational cell is surrounded on all sides by perfectly-matched layer (PML) absorbing boundaries.
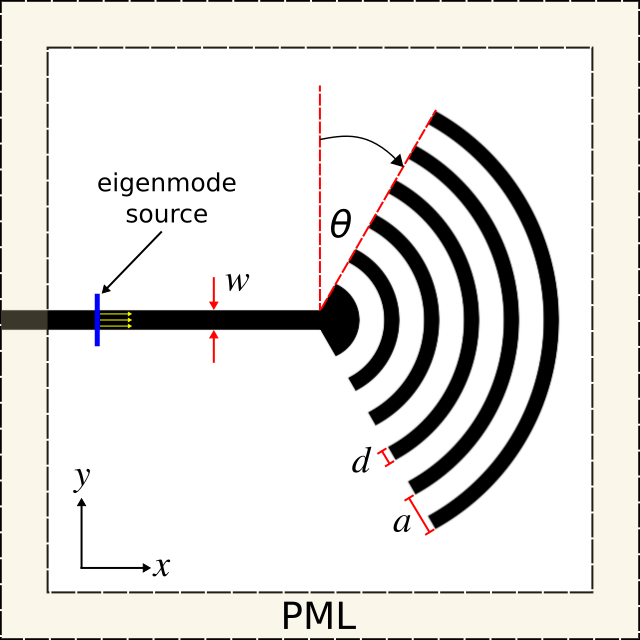
The simulation script consists of the device geometry, source, near-field surface (used to compute the far fields), time-stepping routine, and far-field output. First, the device geometry which includes the Bragg grating, waveguide, and substrate is defined using a combination of various shape objects. The entire structure is parameterized though only two parameters are optimized in this example.
(set-param! resolution 20) ; pixels/μm
(define-param h 0.22) ; waveguide height
(define-param w 0.5) ; waveguide width
(define-param a 1.0) ; Bragg grating periodicity/lattice parameter
(define-param d 0.5) ; Bragg grating thickness
(define-param N 5) ; number of grating periods
(set! N (+ N 1))
(define nSi 3.45)
(define Si (make medium (index nSi)))
(define nSiO2 1.45)
(define SiO2 (make medium (index nSiO2)))
(define-param sxy 16)
(define-param sz 4)
(set! geometry-lattice (make lattice (size sxy sxy sz)))
; rings of Bragg grating
(set! geometry (append geometry
(map (lambda (n)
(list
(make cylinder (material Si) (center 0 0 0) (radius (* n a)) (height h))
(make cylinder (material air) (center 0 0 0) (radius (- (* n a) d)) (height h))))
(arith-sequence N -1 N))))
(set! geometry (apply append geometry))
; remove left half of Bragg grating rings to form semi circle
(set! geometry (append geometry (list
(make block (material air) (center (* -0.5 (* N a)) 0 0) (size (* N a) (* 2 N a) h))
(make cylinder (material Si) (center 0 0 0) (radius (- a d)) (height h)))))
; angle sides of Bragg grating
; rotation angle of sides relative to Y axis (degrees)
(define-param rot-theta 0)
(set! rot-theta (deg->rad (- rot-theta)))
(define pvec (vector3 0 (* 0.5 w) 0))
(define cvec (vector3 (* -0.5 N a) (+ (* 0.5 N a) (* 0.5 w)) 0))
(define rvec (vector3- cvec pvec))
(define rrvec (rotate-vector3 (vector3 0 0 1) rot-theta rvec))
(set! geometry (append geometry (list (make block
(material air)
(center (vector3+ pvec rrvec)) (size (* N a) (* N a) h)
(e1 (rotate-vector3 (vector3 0 0 1) rot-theta (vector3 1 0 0)))
(e2 (rotate-vector3 (vector3 0 0 1) rot-theta (vector3 0 1 0)))
(e3 (vector3 0 0 1))))))
(set! pvec (vector3 0 (* -0.5 w) 0))
(set! cvec (vector3 (* -0.5 N a) (- (+ (* 0.5 N a) (* 0.5 w))) 0))
(set! rvec (vector3- cvec pvec))
(set! rrvec (rotate-vector3 (vector3 0 0 1) (- rot-theta) rvec))
(set! geometry (append geometry (list (make block
(material air)
(center (vector3+ pvec rrvec)) (size (* N a) (* N a) h)
(e1 (rotate-vector3 (vector3 0 0 1) (- rot-theta) (vector3 1 0 0)))
(e2 (rotate-vector3 (vector3 0 0 1) (- rot-theta) (vector3 0 1 0)))
(e3 (vector3 0 0 1))))))
; input waveguide
(set! geometry (append geometry (list
(make block (material air) (center (* -0.25 sxy) (+ (* 0.5 w) (* 0.5 a)) 0) (size (* 0.5 sxy) a h))
(make block (material air) (center (* -0.25 sxy) (- (+ (* 0.5 w) (* 0.5 a))) 0) (size (* 0.5 sxy) a h))
(make block (material Si) (center (* -0.25 sxy) 0 0) (size (* 0.5 sxy) w h)))))
; substrate
(set! geometry (append geometry (list (make block
(material SiO2)
(center 0 0 (+ (* -0.5 sz) (* 0.25 (- sz h))))
(size infinity infinity (* 0.5 (- sz h)))))))
; surround the entire computational cell with PML
(define-param dpml 1.0)
(set! pml-layers (list (make pml (thickness dpml))))
Next, the eigenmode source is defined which is based on calling MPB to compute a definite-frequency mode and using it as the amplitude profile. We use a Gaussian pulsed source, with center wavelength corresponding to 1.55 μm, such that the fields eventually decay away due to absorption by the PMLs and the simulation can be terminated.
; mode frequency
(define-param fcen (/ 1.55))
(set! sources (list (make eigenmode-source
(src (make gaussian-src (frequency fcen) (fwidth (* 0.2 fcen))))
(size 0 (- sxy (* 2 dpml)) (- sz (* 2 dpml)))
(center (+ (* -0.5 sxy) dpml 1.5) 0 0)
(eig-match-freq? true)
(eig-parity ODD-Y))))
We can exploit the mirror symmetry in the structure and the sources to reduce the computation size by a factor of 2.
(set! symmetries (list (make mirror-sym (direction Y) (phase -1))))
We define the near-field surface to span the entire non-PML region above the device, adjacent to the PML in the Z direction.
(define nearfield
(add-near2far fcen 0 1
(make near2far-region (center 0 0 (- (* 0.5 sz) dpml)) (size (- sxy (* 2 dpml)) (- sxy (* 2 dpml)) 0))))
The fields are time stepped until sufficiently decayed.
(run-sources+ (stop-when-fields-decayed 50 Ey (vector3 0 0 0) 1e-6))
Finally, we compute the far fields at 1.55 μm at a series of points on a semicircle within the XZ plane using Meep's near-to-far-field transformation feature. The radius of the semicircle is 1000 wavelengths which is sufficiently large to obtain the far fields. Each far-field point corresponds to an angle, at equally-spaced intervals, from the X axis. The number of far-field points is a parameter with default of 100. The output consists of the six field components (Ex,Ey,Ez,Hx,Hy,Hz) at each point in space.
; far-field radius is 1000 wavelengths from the device center
(define-param r (* 1000 (/ fcen)))
; number of far-field points to compute on the semicircle in XZ
(define-param npts 100)
; print the far-field data for each field component at each point on the semicircle
(map (lambda (n)
(let ((ff (get-farfield nearfield (vector3 (* r (cos (* pi (/ n npts)))) 0 (* r (sin (* pi (/ n npts))))))))
(print "farfield:, " (number->string n) ", " (number->string (* pi (/ n npts))))
(map (lambda (m)
(print ", " (number->string (list-ref ff m))))
(arith-sequence 0 1 6))
(print "\n")))
(arith-sequence 0 1 npts))
With this simulation script, we can now create an objective function used in the nonlinear optimization for device design. In this example, the objective function takes two parameters as input, the grating periodicity and length (as a fraction of the periodicity), and returns the fraction of the far-field radiated power concentrated within the angular cone spanning 70° to 80°. The script invokes the shell to execute a parallel Meep simulation with 8 processors. The output is written to a file. From the far fields, the power in the XZ plane is computed as a function of angle from the X axis.
function [val] = compute_radiated_power(p)
a=p(1);
dfrac=p(2);
d=a*dfrac;
np=8;
rot_theta=20;
system(sprintf("nohup mpirun -np %d meep a=%0.2f d=%0.2f rot-theta=%d bragg_outcoupler.ctl > ...
bragg-optimize-a%0.2f-d%0.2f.out",np,a,d,rot_theta,a,d));
system(sprintf("grep farfield: bragg-optimize-a%0.2f-d%0.2f.out |cut -d , -f2- > ...
bragg-optimize-a%0.2f-d%0.2f.dat",a,d,a,d));
# load far-field data from Meep calculation into arrays for each field component
f = dlmread(sprintf("bragg-optimize-a%0.2f-d%0.2f.dat",a,d),',');
Ex = f(:,2); Ey = f(:,3); Ez = f(:,4);
Hx = f(:,5); Hy = f(:,6); Hz = f(:,7);
# conjugate electric field data
Exc = conj(Ex); Eyc = conj(Ey); Ezc = conj(Ez);
# Poynting vector in Cartesian directions
Px = real(Eyc.*Hz - Ezc.*Hy);
Py = real(Ezc.*Hx - Exc.*Hz);
Pz = real(Exc.*Hy - Eyc.*Hx);
# Poynting vector in XZ plane
Pr = sqrt(Px.^2+Pz.^2);
# minimum cone angle (degrees)
ang_min = 70;
# maximum cone angle (degrees)
ang_max = 80;
ang_min = ang_min*pi/180;
ang_max = ang_max*pi/180;
# normalized in-plane flux in range [0,1]
Pnorm = Pr/max(Pr);
# find the array indices for angular range
idx = find((f(:,1) > ang_min) & (f(:,1) < ang_max));
# fraction of in-plane flux concentrated in angular cone
val = sum(Pnorm(idx))/sum(Pnorm);
disp(sprintf("power:, %0.2f, %0.2f, %0.6f",a,d,val));
fflush(stdout);
return;
Finally, we set up the nonlinear optimization using NLopt by defining the parameter constraints, optimization algorithm, and termination criteria. The initial parameters are chosen randomly. We are using a gradient-free approach since the design involves just two parameters. For designs involving a large number of parameters, a gradient-based approach using adjoint methods would be more efficient. This would enable the use of conjugate gradient methods. The optimization is run multiple times to explore various local optima. A benefit of using NLopt is that we can try several different optimization algorithms by changing just one line in the script. Each solve of the objection function takes approximately 15 minutes on a system with 2.8 GHz AMD Opteron processors.
# lattice parameter (um)
a_min = 0.50;
a_max = 3.00;
# waveguide width (fraction of lattice parameter)
dfrac_min = 0.2;
dfrac_max = 0.8;
opt.algorithm = NLOPT_LN_BOBYQA;
opt.ftol_abs = 0.005;
opt.xtol_abs = 0.02;
opt.maxeval = 50;
opt.verbose = 1;
opt.initial_step = 0.04;
opt.lower_bounds = [ a_min dfrac_min ];
opt.upper_bounds = [ a_max dfrac_max ];
opt.max_objective = @compute_radiated_power;
# random initial parameters
a_0 = a_min + (a_max-a_min)*rand;
dfrac_0 = dfrac_min + (dfrac_max-dfrac_min)*rand;
[xopt, fopt, retcode] = nlopt_optimize(opt,[a_0 dfrac_0]);
disp(sprintf("optimum:, a=%0.2f um, d=%0.2f um",xopt(1),xopt(1)*xopt(2)));
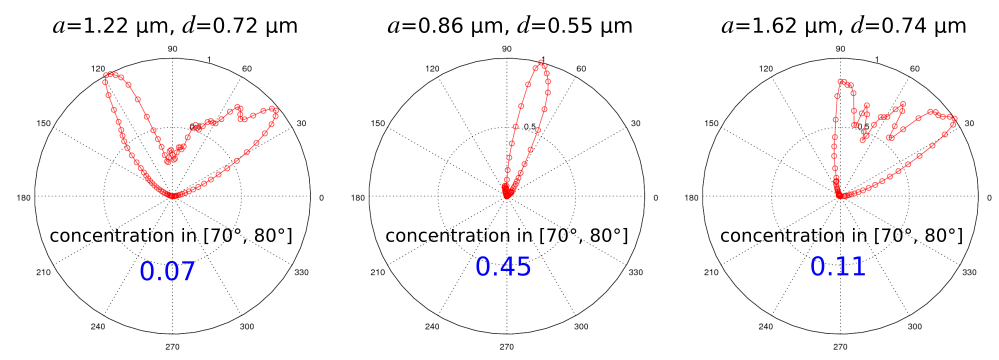
Here are results from the nonlinear optimization for three different local optima found in the search space. Each run took approximately 10 iterations to converge. The polar plot of the far-field energy density is shown for each design. Also shown is the concentration in the angular cone (objective function). The middle inset has just a single lobe in its radiation pattern and thus the highest concentration.
MPB Project #2 — Band Gap of Photonic-Crystal Nanobeam Waveguide
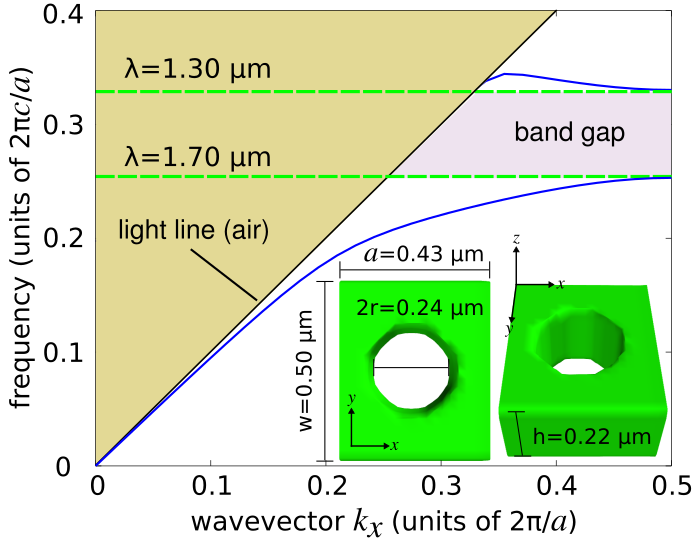
One-dimensional photonic-crystal waveguides consisting of a periodic array of cylindrical holes within a silicon slab of rectangular cross section are found in a wide range of applications involving lasers, optomechanics, and quantum optics. An important feature of these structures is that they can support cavity modes with low losses having quality factors typically exceeding 106 (as demonstrated in the next section) and are simpler to fabricate than their 2d or 3d counterparts. We will use MPB to compute the dispersion relation of a 1d photonic-crystal nanobeam waveguide based on the design in Applied Physics Letters, 94, 121106 (2009) (pdf). This structure can be fabricated using an SOI wafer.A schematic of the waveguide unit cell is shown in the figure below. The lattice periodicity (a) is 0.43 μm and the waveguide width (w) and height (h) are 0.50 and 0.22 μm. The hole radius 0.28a which is 0.12 μm. Given the 1d periodicity, we compute the dispersion relation within the irreducible Brillouin zone which spans axial wavevectors along the X direction from 0 to π/a. This is shown in the figure below. There is a bandgap, a region in which there are no guided modes, in the wavelength range of 1.30-1.70 μm. The light line of air is also shown.
(set-param! resolution 20) ; pixels/a
(define-param a 0.43) ; units of um
(define-param r 0.12) ; units of um
(define-param h 0.22) ; units of um
(define-param w 0.50) ; units of um
(set! r (/ r a)) ; units of "a"
(set! h (/ h a)) ; units of "a"
(set! w (/ w a)) ; units of "a"
(define-param nSi 3.5)
(define Si (make medium (index nSi)))
(set! geometry-lattice (make lattice (size 1 4 4)))
(set! geometry (list (make block (center 0 0 0) (size infinity w h) (material Si))
(make cylinder (center 0 0 0) (radius r) (height infinity) (material air))))
(set! k-points (list (vector3 0 0 0)
(vector3 0.5 0 0)))
(define-param num-kpoints 20)
(set! k-points (interpolate num-kpoints k-points))
(set-param! num-bands 5)
(run-yodd-zeven)
We run the simulation script from the shell terminal, pipe the results to a file, and then grep the relevant contents into a separate file for plotting. This takes a few seconds on a machine with a single 2.8 GHz AMD Opteron processor.
mpb nanobeam-modes.ctl |tee modes.out
grep zevenyoddfreqs: modes.out |cut -d , -f3,7- |sed 1d > modes.dat
Finally, we plot the results using Python.
f = dlmread("modes.dat",',');
plot(f(:,1),f(:,2:end),'b-',f(:,1),f(:,1),'k-');
xlabel("wavevector kx (units of 2\pi/a)");
ylabel("frequency (units of 2\pic/a)");
axis([0 0.5 0 0.4]);
Files: Simulation Script, Shell Launch Script, Plot Results. [gzipped tarball]
Meep Project #3 — Resonant Modes of a Photonic-Crystal Nanobeam Cavity
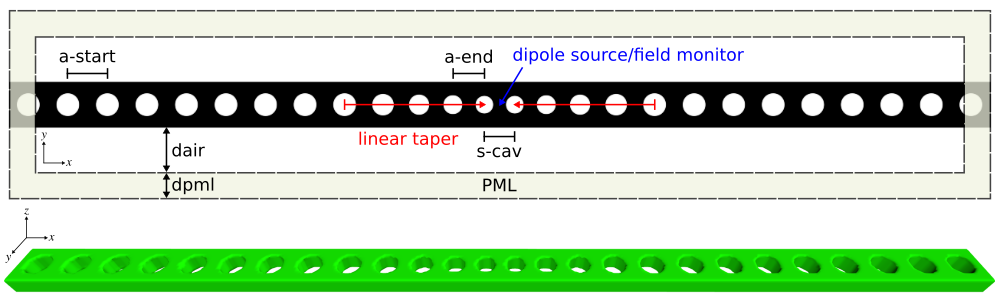
Using the nanobeam waveguide design of the previous section which has a bandgap between 1.30 and 1.70 μm, we proceed to create a resonant cavity by linearly tapering the lattice periodicity from a starting value ofa-start to ending a-end with radii r=0.28a of several holes on either side of a defect as shown in the schematic below. This cavity design is based on the Applied Physics Letters reference from above. We use Meep to design the cavity structure to maximize the quality factor (Q) of the fundamental resonant mode. In this example, there is only one design parameter: the cavity length (s-cav).
(set-param! resolution 40) ; pixels/μm
(define-param a-start 0.43) ; starting periodicity
(define-param a-end 0.33) ; ending periodicity
(define-param s-cav 0.146) ; cavity length
(define-param r 0.28) ; hole radius (units of "a")
(define-param h 0.22) ; waveguide height
(define-param w 0.50) ; waveguide width
(define-param dair 1.00) ; air padding
(define-param dpml 1.00) ; PML thickness
(define-param Ndef 3) ; number of linearly-varying unit cells, excluding starting and ending cells
(define a-taper (interpolate Ndef (list a-start a-end)))
(define a-last (list-ref a-taper (+ Ndef 1)))
(define dgap (- a-last (* 2 r a-last)))
(define-param Nwvg 8) ; number of waveguide unit cells on either side of cavity
(define sx (+ (* 2 (+ (* Nwvg a-start) (fold-left + 0 a-taper))) (- dgap) s-cav))
(define sy (+ dpml dair w dair dpml))
(define sz (+ dpml dair h dair dpml))
(set! geometry-lattice (make lattice (size sx sy sz)))
(set! pml-layers (list (make pml (thickness dpml))))
(define-param nSi 3.5)
(define Si (make medium (index nSi)))
(set! geometry (list (make block (center 0 0 0) (size infinity w h) (material Si))))
(define holes (list '()))
(set! holes (append holes
(map (lambda (mm) (list
(make cylinder (center (+ (* -0.5 sx) (* 0.5 a-start) (* mm a-start)) 0 0) (radius (* r a-start))
(height infinity) (material air))
(make cylinder (center (- (* 0.5 sx) (* 0.5 a-start) (* mm a-start)) 0 0) (radius (* r a-start))
(height infinity) (material air))))
(arith-sequence 0 1 Nwvg))))
(set! holes (apply append holes))
(set! geometry (append geometry holes))
(set! holes (list '()))
(set! holes (append holes
(map (lambda (mm) (list
(make cylinder (center (+ (* -0.5 sx) (* Nwvg a-start)
(if (> mm 0) (fold-left + 0 (map (lambda (nn) (list-ref a-taper nn)) (arith-sequence 0 1 mm))) 0) (* 0.5 (list-ref a-taper mm))) 0 0)
(radius (* r (list-ref a-taper mm))) (height infinity) (material air))
(make cylinder (center (- (* 0.5 sx) (* Nwvg a-start)
(if (> mm 0) (fold-left + 0 (map (lambda (nn) (list-ref a-taper nn)) (arith-sequence 0 1 mm))) 0) (* 0.5 (list-ref a-taper mm))) 0 0)
(radius (* r (list-ref a-taper mm))) (height infinity) (material air))))
(arith-sequence 0 1 (+ Ndef 2)))))
(set! holes (apply append holes))
(set! geometry (append geometry holes))
(define-param lambda-min 1.46) ; minimum source wavelength
(define-param lambda-max 1.66) ; maximum source wavelength
(define fmin (/ lambda-max)) ; minimum source frequency
(define fmax (/ lambda-min)) ; maximum source frequency
(define fcen (* 0.5 (+ fmin fmax))) ; source frequency center
(define df (- fmax fmin)) ; source frequency width
(set! sources (list (make source (src (make gaussian-src (frequency fcen) (fwidth df))) (component Ey) (center 0 0 0))))
(set! symmetries (list (make mirror-sym (direction X) (phase +1))
(make mirror-sym (direction Y) (phase -1))
(make mirror-sym (direction Z) (phase +1))))
(define-param src-time 800)
(run-sources+ src-time (after-sources (harminv Ey (vector3 0 0 0) fcen df))
(in-volume (volume (center 0 0 0) (size sx sy 0)) (at-end output-epsilon output-efield-y)))
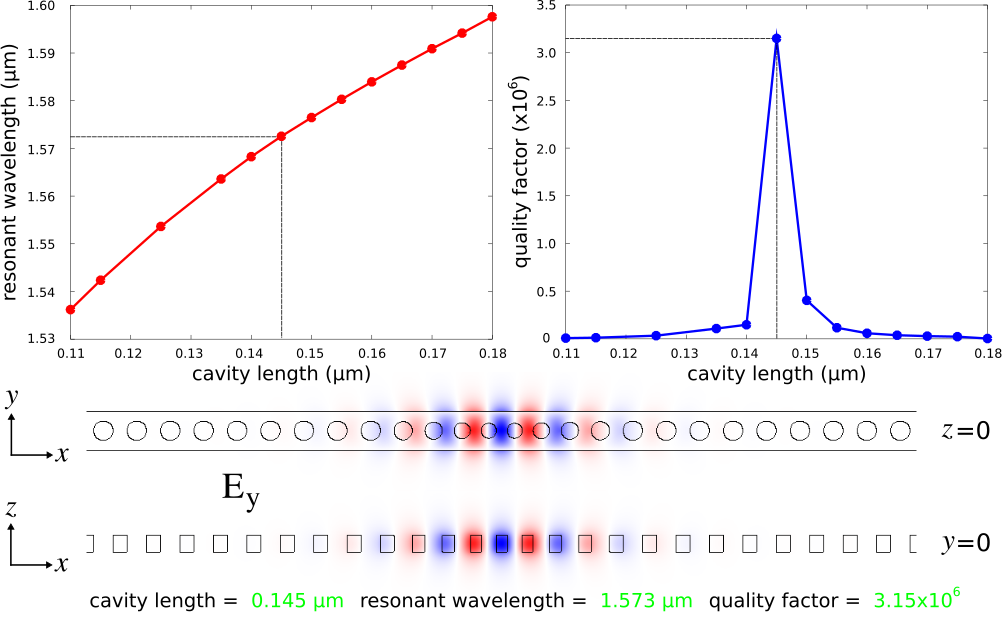
A bash script is used to sweep the cavity length (s-cav) over the range of 0.110-0.180 μm in increments of 0.005 μm. The output is written to a file with the harminv-related information extracted to a different file for plotting. The figures below show a plot of the resonant wavelength and quality factor as a function of the cavity length. The quality factor is maximum for the design with a cavity length of 0.145 μm. These are consistent with the values reported in the reference.
#!/bin/bash
for scav in `seq 0.110 0.005 0.180`; do
mpirun -np 2 meep s-cav=${scav} nanobeam.ctl > nanobeam_cavity_length${scav}.out;
grep harminv0: nanobeam_cavity_length${scav}.out |cut -d , -f2,4 |grep -v frequency >> nanobeam_cavity_varylength.dat;
done;
The Ey field profile for the optimal design of the fundamental cavity mode is also shown below for two cross sections. The resonant mode is confined by the bandgap in the direction of the holes (X) and index guiding in the Y and Z directions. These images were created using h5utils from the shell terminal as follows:
h5topng -o cavity_field_profile.png -C nanobeam-eps-000040000.h5 -vZc bluered nanobeam-ey-000040000.h5
Meep Project #4 — Near-Infrared Absorption Spectra of CMOS Image Sensors
Complimentary metal oxide semiconductor (CMOS) image sensors are widely used in camera modules of mobile devices due to their lower power consumption and better electrical-readout capabilities than charge-coupled device (CCD) sensors. CMOS image sensors for visible light have recently been extended to the near infrared (IR) for applications including biomedicine, security, and chemical spectroscopy. The design challenge involves enhancing the light trapping of individual pixels at near-IR wavelengths where the absorption coefficient of silicon is small.We will investigate the back-illuminated CMOS image-sensor pixel design based on the work of Sony researchers presented in Scientific Reports, Vol. 7, No. 3832, 2017. A glass microlens (silicon dioxide) with a radius of curvature of 0.85 μm is placed on the top of the image sensor. This is necessary for focusing incident light from air into the individual pixels. A metal aperture grid made of a tungsten wire with rectangular cross section (width: 0.1 μm, height: 0.2 μm) surrounds the pixel and is placed on top of the semi-infinite crystalline-silicon substrate (thickness: 3 μm, indirect bandgap: 1.108 μm). A color filter for red, green, and blue light, which in standard designs is placed above the metal grid, is neglected in this structure. A square lattice of inverted cones on the front surface of the substrate is used to scatter the incident light in order to increase the optical path length. Deep-trench isolation is used to mitigate electrical cross talk between adjacent pixels as well as to trap photons via index guiding. This involves surrounding the pixel with a silicon-dioxide trench (width: 0.1 μm, thickness: 2 μm). A schematic of the unit-cell cross section of a single pixel is shown in the left figure below. The right figure shows the square lattice of inverted cones in the unit cell. For a broadband spectrum spanning near-IR wavelengths of 0.7 to 1.0 μm, we will use Meep to compute three device properties: (1) reflection from the top surface, (2) absorption of the tungsten wires, and (3) absorption of the silicon substrate. We will investigate the enhancement of the substrate absorption due to different lattice structures relative to a flat substrate. The design objective is to find the lattice design which maximizes the substrate absorption averaged over the entire spectrum.
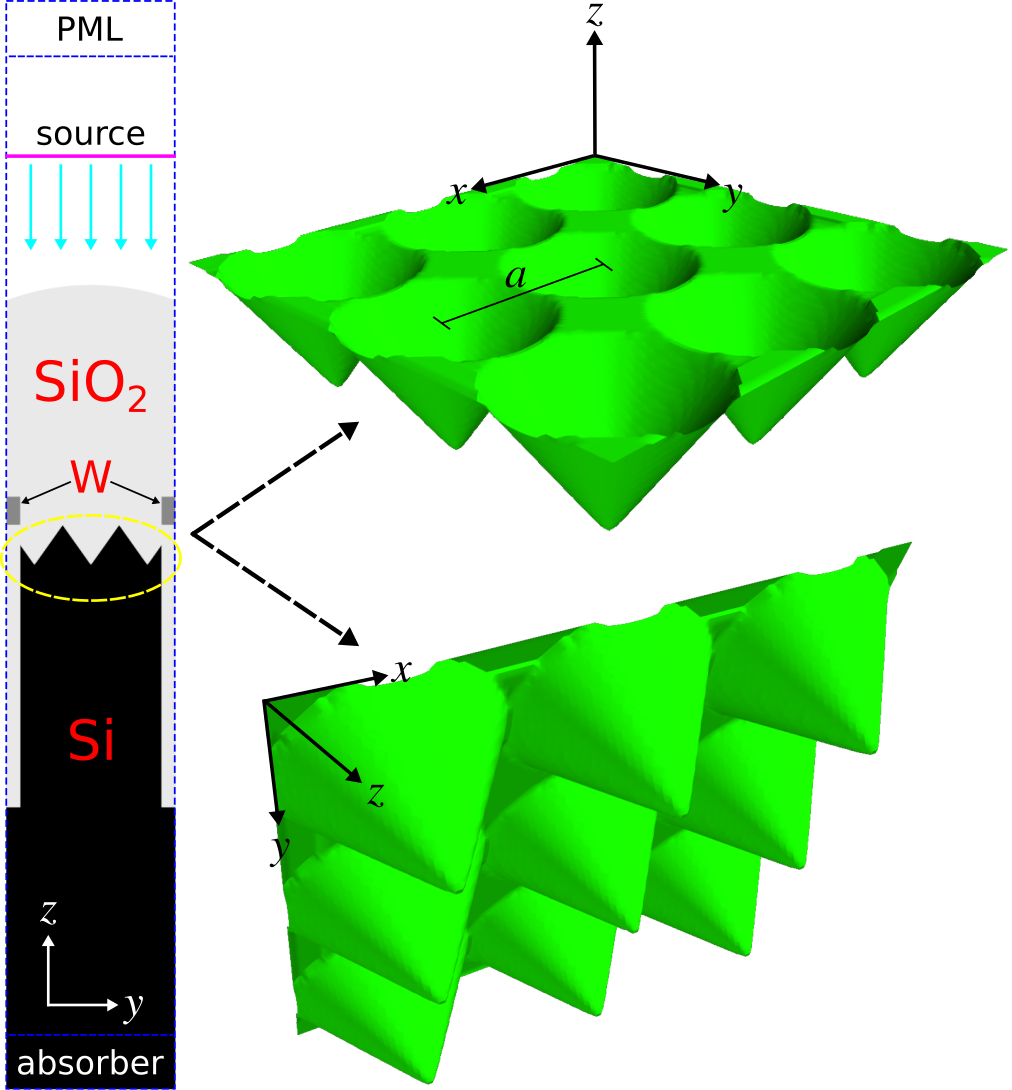
The Meep simulation script has three main components: (1) defining the tungsten and silicon material parameters over the broadband wavelength spectrum, (2) setting up the supercell geometry involving a square lattice of inverted cones, and (3) computing the absorption of the metal grid and the substrate via the the total flux within these regions. The silicon material parameters are obtained by fitting the experimental values for crystalline silicon over the near-IR wavelength spectrum to a single Lorentzian-susceptibility term and adding a small imaginary component. This is explained in the supplementary-information section of Applied Physics Letters, Vol. 104, No. 091121, 2014 (pdf). All materials are included in Meep's materials library. A normally-incident planewave in air above the device is used as the source. The supercell lattice contains 3×3 unit cells with periodic boundary conditions. Four flux planes are used: one for reflection and three for transmission. The absorption is calculated as the difference in the flux entering and exiting each region (normalized by the total flux from just the source). This way, we can calculate the absorption over the entire broadband spectrum for any number of rectilinear regions using a single simulation.
(set-param! resolution 30) ; pixels/μm
(define-param a 0.4) ; lattice periodicity
(define cone-r (* 0.5 a)) ; cone radius
(define cone-h (* cone-r (tan (deg->rad 54.7)))) ; cone height
(define-param wire-w 0.1) ; wire width
(define-param wire-h 0.2) ; wire height
(define-param trench-w 0.1) ; trench width
(define-param trench-h 2.0) ; trench height
(define-param dair 1.0) ; air gap thickness
(define-param dmcl 1.7) ; micro lens thickness
(define-param dsub 3.0) ; substrate thickness
(define-param dabs 1.0) ; absorber thickness
(define-param np 3) ; number of periods
(define sxy (* np a))
(define sz (+ dabs dair dmcl dsub dabs))
(set! geometry-lattice (make lattice (size sxy sxy sz)))
(set! pml-layers (list (make pml (thickness dabs) (direction Z) (side High))
(make absorber (thickness dabs) (direction Z) (side Low))))
(define-param substrate? true)
(if substrate?
(set! geometry (list
(make sphere (material SiO2) (radius dmcl) (center 0 0 (- (* 0.5 sz) dabs dair dmcl)))
(make block (material cSi) (size infinity infinity (+ dsub dabs))
(center 0 0 (+ (* -0.5 sz) (* 0.5 (+ dsub dabs)))))
(make block (material W) (size infinity wire-w wire-h)
(center 0 (+ (* -0.5 sxy) (* 0.5 wire-w)) (+ (* -0.5 sz) dabs dsub (* 0.5 wire-h))))
(make block (material W) (size infinity wire-w wire-h)
(center 0 (- (* 0.5 sxy) (* 0.5 wire-w)) (+ (* -0.5 sz) dabs dsub (* 0.5 wire-h))))
(make block (material W) (size wire-w infinity wire-h)
(center (+ (* -0.5 sxy) (* 0.5 wire-w)) 0 (+ (* -0.5 sz) dabs dsub (* 0.5 wire-h))))
(make block (material W) (size wire-w infinity wire-h)
(center (- (* 0.5 sxy) (* 0.5 wire-w)) 0 (+ (* -0.5 sz) dabs dsub (* 0.5 wire-h)))))))
(define-param texture? false)
(if (and substrate? texture?)
(map (lambda (nx)
(map (lambda (ny)
(let ((cx (+ (* -0.5 sxy) (* (+ nx 0.5) a)))
(cy (+ (* -0.5 sxy) (* (+ ny 0.5) a))))
(set! geometry (append geometry
(list (make cone (material SiO2) (radius 0) (radius2 r) (height h)
(center cx cy (- (* 0.5 sz) dabs dair dmcl (* 0.5 h)))))))))
(arith-sequence 0 1 np)))
(arith-sequence 0 1 np)))
(set! geometry (append geometry (list
(make block (material SiO2) (size infinity trench-w trench-h)
(center 0 (+ (* -0.5 sxy) (* 0.5 trench-w)) (- (* 0.5 sz) dabs dair dmcl (* 0.5 trench-h))))
(make block (material SiO2) (size infinity trench-w trench-h)
(center 0 (- (* 0.5 sxy) (* 0.5 trench-w)) (- (* 0.5 sz) dabs dair dmcl (* 0.5 trench-h))))
(make block (material SiO2) (size trench-w infinity trench-h)
(center (+ (* -0.5 sxy) (* 0.5 trench-w)) 0 (- (* 0.5 sz) dabs dair dmcl (* 0.5 trench-h))))
(make block (material SiO2) (size trench-w infinity trench-h)
(center (- (* 0.5 sxy) (* 0.5 trench-w)) 0 (- (* 0.5 sz) dabs dair dmcl (* 0.5 trench-h)))))))
(set! k-point (vector3 0 0 0))
(define-param lmin 0.7)
(define-param lmax 1.0)
(define fmin (/ lmax))
(define fmax (/ lmin))
(define fcen (* 0.5 (+ fmin fmax)))
(define df (- fmax fmin))
(set! sources (list (src (make source (src (make gaussian-src (frequency fcen) (fwidth df)))
(component Ex) (center 0 0 (- (* 0.5 sz) dabs (* 0.5 dair))) (size sxy sxy 0)))))
(define-param nfreq 50)
(define refl (add-flux fcen df nfreq (make flux-region (center 0 0 (- (* 0.5 sz) dabs)) (size sxy sxy 0))))
(define trans-grid (add-flux fcen df nfreq (make flux-region (center 0 0 (+ (* -0.5 sz) dabs dsub wire-h)) (size sxy sxy 0))))
(define trans-sub-top (add-flux fcen df nfreq (make flux-region (center 0 0 (+ (* -0.5 sz) dabs dsub)) (size sxy sxy 0))))
(define trans-sub-bot (add-flux fcen df nfreq (make flux-region (center 0 0 (+ (* -0.5 sz) dabs)) (size sxy sxy 0))))
(if substrate? (load-minus-flux "refl-flux" refl))
(run-sources+ (stop-when-fields-decayed 50 Ex (vector3 0 0 (+ (* -0.5 sz) dabs (* 0.5 dsub))) 1e-9))
(if (not substrate?) (save-flux "refl-flux" refl))
(display-fluxes refl trans-grid trans-sub-top trans-sub-bot)
We will create a Bash shell script to run three simulations for each lattice design: (1) the empty cell with just the source, (2) the flat substrate, and (3) the textured substrate. The lattice periodicity (a) is varied over the range of 0.40 to 0.70 μm. The simulation output is piped to a file for post processing in Python or Octave/Matlab.
#!/bin/bash
for a in `seq 0.40 0.02 0.70`; do
mpirun -np 4 meep a=${a} substrate?=false cmos-sensor.ctl > cmos_a${a}_empty.out;
grep flux1: cmos_a${a}_empty.out |cut -d , -f2- > cmos_a${a}_empty.dat;
mpirun -np 4 meep a=${a} substrate?=true texture?=false cmos-sensor.ctl > cmos_a${a}_flat.out;
grep flux1: cmos_a${a}_flat.out |cut -d , -f2- > cmos_a${a}_flat.dat;
mpirun -np 4 meep a=${a} substrate?=true texture?=true cmos-sensor.ctl > cmos_a${a}_texture.out;
grep flux1: cmos_a${a}_texture.out |cut -d , -f2- > cmos_a${a}_texture.dat;
done;
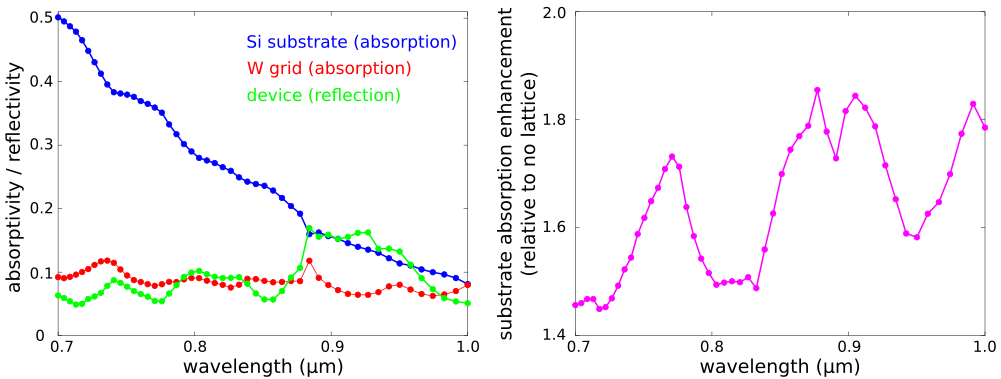
The left figure below is a contour plot of the substrate absorption as a function of wavelength and lattice periodicity. This is the fraction of the incident light which is absorbed by just the crystalline-silicon substrate. For all lattice designs, the absorption is largest at the smallest wavelengths which is expected. The right figure shows the enhancement of the substrate absorption due to the lattice relative to a flat substrate (i.e., no lattice). The lattice produces wavelength-dependent scattering effects which can be seen as the dark spots in the contour plot.
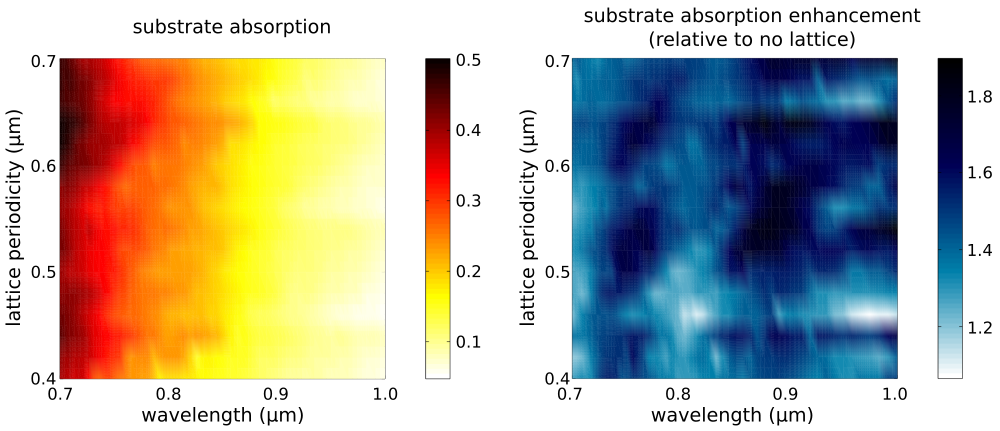
The optimal lattice design which has the largest average absorption over the broadband spectrum is a=0.64 μm with 24.5%±12.2%. A plot of the substrate and grid absorption as well as the reflection from the device for this lattice design are shown in the left figure below. For comparison, the average substrate absorption for the no-lattice reference design is 15.4%±8.5%. The optimal lattice yields an average enhancement per wavelength of 1.6±0.6.
Files: Simulation Script, Shell Launch Script, Post Processing. [gzipped tarball]
Meep Project #5 — Thermal Radiation Spectra of Plasmonic Metamaterials
We can use Meep to compute the thermal-radiation spectra of metallic devices. This is based on Kirchhoff's law of thermal radiation which states that for an arbitrary body emitting and absorbing thermal radiation in thermodynamic equilibrium, the emissivity is equal to the absorptivity. Computing the emissivity (or emittance) of the device is therefore equivalent to computing its absorptivity (or absorptance). The thermal radiation spectra of the device is the product of its absorptance with the black body radiation spectrum given by Planck's law.The schematic below shows the unit cell geometry of a plasmonic metamaterial. The design is based on J. Optical Society of America B, Vol. 30, pp. 165-172, 2013. The structure consists of a square lattice of cylindrical Platinum (Pt) rods on top of a semi-infinite silicon substrate. In a real experiment, Joule or Convective heating would be applied to the Pt layer and the thermal radiation measured using an infrared camera. In the simulation, a planewave is normally incident from the air region above the device. Periodic boundary conditions are used in the xy plane and perfectly-matched layers (PMLs) in the transverse z direction. The absorptance can be obtained as simply 1-reflectance, using a single flux monitor as shown in the schematic. There is no transmission through the Pt layer into the substrate since the incident planewave is either reflected from the device or absorbed by surface-plasmon polaritons.
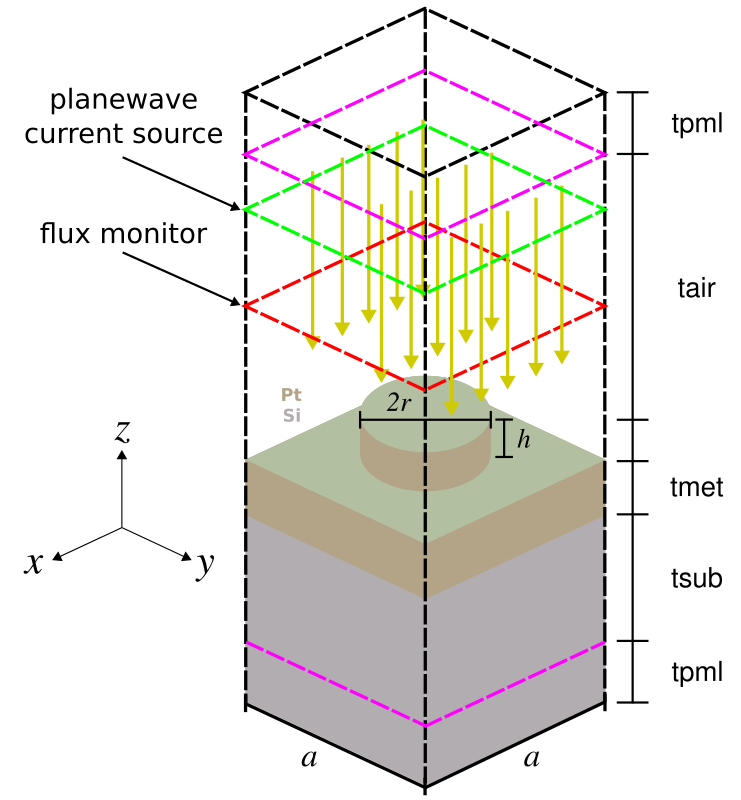
The design objective, for applications such as sensing, is to find a lattice geometry which has a single emission peak with minimum bandwidth and maximum amplitude in the near-infrared wavelength range (i.e., 2-5 μm). There are two degrees of freedom: the lattice periodicity (a) and rod radius (r). The rod height (h) is fixed. Given the small number of parameters, we can explore the entire design space using a brute-force search. The simulation script, shell launch script, and sample results are shown below.
(set-param! eps-averaging? true)
(set-param! resolution 40) ; pixels/um
(define-param a 4.5) ; lattice periodicity
(define-param r 1.5) ; metal rod radius
(define-param h 0.2) ; metal rod height
(define-param tmet 0.3) ; metal layer thickness
(define-param tsub 2.0) ; substrate thickness
(define-param tabs 5.0) ; absorber thickness
(define-param tair 4.0) ; air thickness
(define sz (+ tabs tair h tmet tsub tabs))
(set! geometry-lattice (make lattice (size a a sz)))
(set! pml-layers (list (make pml (thickness tabs) (direction Z))))
(define lmin 2.0) ; source min wavelength
(define lmax 5.0) ; source max wavelength
(define fmin (/ lmax)) ; source min frequency
(define fmax (/ lmin)) ; source max frequency
(define fcen (* 0.5 (+ fmin fmax)))
(define df (- fmax fmin))
(define Si (make medium (index 3.5)))
(define-param empty? true)
(if (not empty?)
(set! geometry (list
(make cylinder (material Pt) (radius r) (height h) (center 0 0 (- (* 0.5 sz) tabs tair (* 0.5 h))))
(make block (material Pt) (size infinity infinity tmet)
(center 0 0 (- (* 0.5 sz) tabs tair h (* 0.5 tmet))))
(make block (material Si) (size infinity infinity (+ tsub tabs))
(center 0 0 (- (* 0.5 sz) tabs tair h tmet (* 0.5 (+ tsub tabs))))))))
; CCW rotation angle (degrees) about Y-axis of PW current source; 0 degrees along -z axis
(define-param theta 0)
(set! theta (deg->rad theta))
; k with correct length (plane of incidence: XZ)
(define k (vector3-scale fcen (vector3 (sin theta) 0 (cos theta))))
(set! k-point k) ; PBC in XY plane (in units of 2\pi)
(define (pw-amp k x0) (lambda (x) (exp (* 0+1i 2 pi (vector3-dot k (vector3+ x x0))))))
(define src-pos (- (* 0.5 sz) tabs (* 0.2 tair)))
(set! sources (list (make source
(src (make gaussian-src (frequency fcen) (fwidth df)))
(component Ey) (center 0 0 src-pos) (size a a 0)
(amp-func (pw-amp k (vector3 0 0 src-pos))))))
(define-param nfreq 50)
(define refl (add-flux fcen df nfreq (make flux-region (center 0 0 (- (* 0.5 sz) tabs (* 0.5 tair))) (size a a 0))))
(if (not empty?) (load-minus-flux "refl-flux" refl))
(run-sources+ (stop-when-fields-decayed 25 Ey (vector3 0 0 (- (* 0.5 sz) tabs (* 0.5 tair))) 1e-7))
(if empty? (save-flux "refl-flux" refl))
(display-fluxes refl)
#!/bin/bash
np=20;
for a in `seq 4.1 0.1 5.0`; do
mpirun -np ${np} meep empty?=true a=${a} emitter.ctl > flux0_a${a}.out;
grep flux1: flux0_a${a}.out |cut -d , -f2- > flux0_a${a}.dat;
for r_frac in `seq 0.1 0.1 0.4`; do
r=$(printf "%0.2f" `echo "${a}*${r_frac}" |bc`);
mpirun -np ${np} meep empty?=false a=${a} r=${r} emitter.ctl > flux_a${a}_r${r}.out;
grep flux1: flux_a${a}_r${r}.out |cut -d , -f2- > flux_a${a}_r${r}.dat;
done;
done;
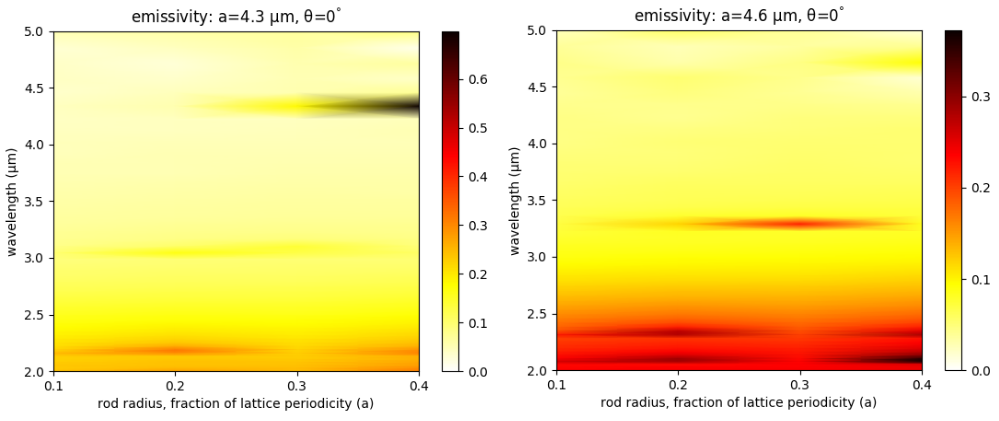
Note that this emissivity calculation is for the thermal radiation directed in the upward direction. To compute the thermal radiation in the downward direction (which is mainly considered loss), we would need to do a separate calculation to obtain the emissivity in the downward direction. This would involve sending a planewave from the bottom of the computational cell and computing the absorptance using the same approach involving the reflectance. The fraction of the total radiation which is directed upward is then the ratio of the emissivity in the upward direction over the sum of the emissivities in the upward and downward directions.
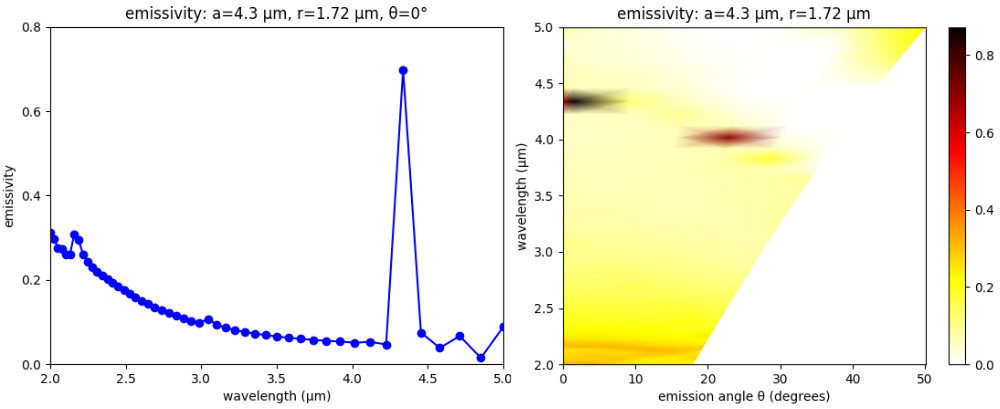
We can also compute the thermal radiation spectra at an oblique angle θ. This is given by equation 63.24 on page 189 of Statistical Physics, Third Edition, 1980 by L.D. Landau and E.M. Lifshitz as: e'(λ)cos(θ)A(λ,θ), where e'(λ) is the black body emission spectrum and A(λ,θ) is the absorptance. We compute the angular radiation spectra cos(θ)A(λ,θ) in the range [0°, 30°] for the metamaterial design with a=4.3 μm and r=1.72 μm. This structure has a single, narrowband emissivity peak of nearly 0.8 at a wavelength of 4.4 μm which is shown in the left figure below.
The following are the shell launch script and Octave/Matlab plotting script.
#!/bin/bash
np=20;
a=4.3;
r=1.72;
for t in `seq 0 5 30`; do
mpirun -np ${np} meep emitter.ctl empty?=true a=${a} theta=${t} > flux0_a${a}_theta${t}.out;
grep flux1: flux0_a${a}_theta${t}.out |cut -d , -f2- > flux0_a${a}_theta${t}.dat;
mpirun -np ${np} meep emitter.ctl empty?=false a=${a} r=${r} theta=${t} > flux_a${a}_r${r}_theta${t}.out;
grep flux1: flux_a${a}_r${r}_theta${t}.out |cut -d , -f2- > flux_a${a}_r${r}_theta${t}.dat;
done;
lmin = 2.0; # source min wavelength
lmax = 5.0; # source max wavelength
fmin = 1/lmax; # source min frequency
fmax = 1/lmin ; # source max frequency
fcen = 0.5*(fmin+fmax);
thetas = [0:5:30];
kx = fcen*sind(thetas);
Refl = zeros(50,length(thetas));
Abs = zeros(50,length(thetas));
theta_out = zeros(50,length(thetas));
for k = 1:length(thetas)
f0 = dlmread(sprintf("flux0_a4.3_theta%d.dat",thetas(k)),",");
f = dlmread(sprintf("flux_a4.3_r1.72_theta%d.dat",thetas(k)),",");
Refl(:,k) = -f(:,2)./f0(:,2);
theta_out(:,k) = asind(kx(k)./f0(:,1));
Abs(:,k) = (1-Refl(:,k)).*cosd(theta_out(:,k));
endfor
Abs(Abs < 0) = 0;
wvl = 1./f0(:,1);
wvls = repmat(wvl,1,length(thetas));
pcolor(theta_out, wvls, Abs);
shading flat; c = colormap("hot"); colormap(flipud(c)); colorbar;
eval(sprintf("axis([%0.2g %0.2g %0.2g %0.2g])",min(min(theta_out)),max(max(theta_out)),min(wvl),max(wvl)));
set(gca, 'xtick', [0:10:50]);
set(gca, 'ytick', [2.0:0.5:5.0]);
xlabel("emission angle (degrees)");
ylabel("wavelength (um)");
title("emissivity: a=4.3 um, r=1.72 um");
Meep Project #6 — Bidirectional Scattering Distribution Function (BSDF) of Asymmetric Gratings
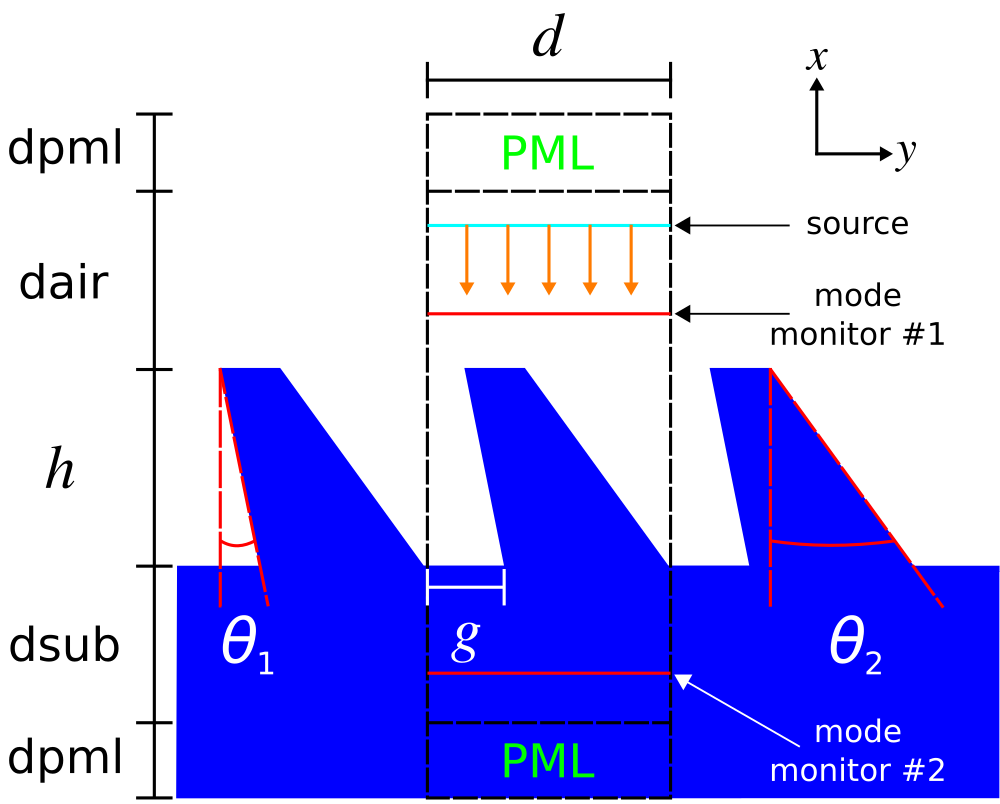
In this example, we use Meep to compute the bidirectional scattering distribution function (BSDF) of a diffraction grating. BSDFs are used in ray tracing for physically based rendering of textured surfaces with wavelength or sub-wavelength (i.e., micro- or nano-scale) features. The BSDF of a grating involves computing the reflectance and transmittance at a single wavelength for all possible diffraction orders (or "rays") for an incident planewave source over a range of angles. This calculation is similar to the Meep tutorial example for a binary grating.The asymmetric grating design, shown in the schematic below along with the overall simulation geometry, is based on Optics Express, Vol. 15, pp. 2067-74, 2007. The unit cell has five degrees of freedom: periodicity (d), height (h), gap (g), and two angles for the side walls (θ1 and θ2). These have arbitrary default values of 3.5 μm, 1.9 μm, 0.7 μm, 12.8°, and 27.4°. The grating material is episulfide with a wavelength-independent refractive index of 1.716. A planewave pulse centered at 0.5 μm is incident from the air region above the grating. The planewave's angle and polarization are specified using the
src-angle and src-pol command-line parameters. Two mode monitors are used to compute the reflectance and transmittance of the diffracted orders via mode decomposition. Note that for any polarized planewave at normal incidence, the asymmetric grating yields diffraction orders which are either even or odd. To separate these modes in the output, we must invoke get-eigenmode-coefficients twice with its eig-parity parameter set to EVEN-Y or ODD-Y. The reflectance and transmittance of each diffracted order is output on separate lines, including its angle, prefixed by refl: and tran:. At the end of the simulation, the total reflectance and transmittance are output on the line prefixed by total:.
(set-param! resolution 50) ; pixels/um
(define-param dpml 1.0) ; PML length
(define-param dair 4.0) ; padding length between PML and grating
(define-param dsub 3.0) ; substrate thickness
(define-param d 3.5) ; grating period
(define-param h 1.9) ; grating height
(define-param g 0.7) ; grating duty cycle
(define-param theta-1 12.8) ; grating sidewall angle #1
(define-param theta-2 27.4) ; grating sidewall angle #2
(set! theta-1 (deg->rad theta-1))
(set! theta-2 (deg->rad theta-2))
(define sx (+ dpml dair h dsub dpml))
(define sy d)
(define cell (make lattice (size sx sy no-size)))
(set! geometry-lattice cell)
(define boundary-layers (list (make absorber (thickness dpml) (direction X))))
(set! pml-layers boundary-layers)
(define-param wvl 0.5) ; center wavelength
(define fcen (/ wvl)) ; center frequency
(define df (* 0.05 fcen)) ; frequency width
(define-param src-pol 1) ; source polarization (1: Ez, 2: Hz, default: Ez)
(define src-cmpt (if (= src-pol 1) Ez Hz))
(define eparity (if (= src-pol 1) ODD-Z EVEN-Z))
; rotation angle (degrees) of incident planewave source; counter clockwise (CCW) about Z axis, 0 degrees along +X axis
(define-param src-angle 0)
(set! src-angle (deg->rad src-angle))
(define k (rotate-vector3 (vector3 0 0 1) src-angle (vector3 fcen 0 0)))
(set! k-point k)
(define (pw-amp k x0)
(lambda (x)
(exp (* 0+1i 2 pi (vector3-dot k (vector3- x x0))))))
(define src-pt (vector3 (+ (* -0.5 sx) dpml (* 0.2 dair)) 0 0))
(define pulse-src (list (make source
(src (make gaussian-src (frequency fcen) (fwidth df)))
(component src-cmpt)
(center (+ (* -0.5 sx) dpml (* 0.5 dsub)) 0 0)
(size 0 sy 0)
(amp-func (pw-amp k src-pt)))))
(set! sources pulse-src)
(define refl-pt (vector3 (+ (* -0.5 sx) dpml (* 0.7 dair)) 0 0))
(define src-flux (add-flux fcen 0 1 (make flux-region (center refl-pt) (size 0 sy 0))))
(run-sources+ 100)
(save-flux "flux" src-flux)
(define input-flux (get-fluxes src-flux))
(reset-meep)
(set! geometry-lattice cell)
(set! pml-layers boundary-layers)
(set! sources pulse-src)
(set! k-point k)
(define ng 1.716) ; episulfide refractive index @ 0.532 μm
(define glass (make medium (index ng)))
(set! geometry (list (make block
(material glass)
(size (+ dpml dsub) infinity infinity)
(center (- (* 0.5 sx) (* 0.5 (+ dpml dsub))) 0 0))
(make prism
(material glass)
(vertices (list
(vector3 (- (* 0.5 sx) dpml dsub) (* 0.5 sy) 0)
(vector3 (- (* 0.5 sx) dpml dsub h) (- (* 0.5 sy) (* h (tan theta-2))) 0)
(vector3 (- (* 0.5 sx) dpml dsub h) (+ (* -0.5 sy) g (* (- h) (tan theta-1))) 0)
(vector3 (- (* 0.5 sx) dpml dsub) (+ (* -0.5 sy) g))))
(axis 0 0 1)
(center auto-center)
(height infinity))))
(define refl-flux (add-flux fcen 0 1 (make flux-region (center refl-pt) (size 0 sy 0))))
(load-minus-flux "flux" refl-flux)
(define tran-pt (vector3 (- (* 0.5 sx) dpml (* 0.5 dsub)) 0 0))
(define tran-flux (add-flux fcen 0 1 (make flux-region (center tran-pt) (size 0 sy 0))))
(run-sources+ 500) ; (at-beginning output-epsilon))
(define kdom-tol 1e-2)
(define angle-tol 1e-6)
(define modulo-float (lambda (n1 n2) (- n1 (* (floor (/ n1 n2)) n2))))
(define res (get-eigenmode-coefficients refl-flux (list 1) #:eig-parity eparity))
(define coeffs (list-ref res 0))
(define kdom (list-ref res 3))
(define Rsum 0)
(define r-angle 0)
(define Tsum 0)
(define t-angle 0)
(if (= src-angle 0)
(let
((nm-r (* 0.5 (- (floor (* (- fcen (vector3-y k)) d)) (ceiling (* (- (- fcen) (vector3-y k)) d)))))
(nm-t (* 0.5 (- (floor (* (- (* fcen ng) (vector3-y k)) d)) (ceiling (* (- (- (* fcen ng)) (vector3-y k)) d))))))
(set! res (get-eigenmode-coefficients refl-flux (arith-sequence 1 1 nm-r) #:eig-parity (+ eparity EVEN-Y)))
(set! coeffs (list-ref res 0))
(set! kdom (list-ref res 3))
(map (lambda (nm)
(let ((r-kdom (list-ref kdom nm))
(Rmode (/ (sqr (magnitude (array-ref coeffs nm 0 1))) (list-ref input-flux 0))))
(if (> (vector3-x r-kdom) kdom-tol)
(begin
(set! r-angle (if (> (modulo-float (vector3-x r-kdom) fcen) angle-tol)
(* (if (positive? (vector3-y r-kdom)) +1 -1) (acos (/ (vector3-x r-kdom) fcen))) 0))
(print "refl: (even-y), " nm ", " (rad->deg r-angle) ", " Rmode "\n")
(set! Rsum (+ Rsum Rmode))))))
(arith-sequence 0 1 nm-r))
(set! res (get-eigenmode-coefficients refl-flux (arith-sequence 1 1 nm-r) #:eig-parity (+ eparity ODD-Y)))
(set! coeffs (list-ref res 0))
(set! kdom (list-ref res 3))
(map (lambda (nm)
(let ((r-kdom (list-ref kdom nm))
(Rmode (/ (sqr (magnitude (array-ref coeffs nm 0 1))) (list-ref input-flux 0))))
(if (> (vector3-x r-kdom) kdom-tol)
(begin
(set! r-angle (if (> (modulo-float (vector3-x r-kdom) fcen) angle-tol)
(* (if (positive? (vector3-y r-kdom)) +1 -1) (acos (/ (vector3-x r-kdom) fcen))) 0))
(print "refl: (odd-y), " nm ", " (rad->deg r-angle) ", " Rmode "\n")
(set! Rsum (+ Rsum Rmode))))))
(arith-sequence 0 1 nm-r))
(set! res (get-eigenmode-coefficients tran-flux (arith-sequence 1 1 nm-t) #:eig-parity (+ eparity EVEN-Y)))
(set! coeffs (list-ref res 0))
(set! kdom (list-ref res 3))
(map (lambda (nm)
(let ((t-kdom (list-ref kdom nm))
(Tmode (/ (sqr (magnitude (array-ref coeffs nm 0 0))) (list-ref input-flux 0))))
(if (> (vector3-x t-kdom) kdom-tol)
(begin
(set! t-angle (if (> (modulo-float (vector3-x t-kdom) (* fcen ng)) angle-tol)
(* (if (positive? (vector3-y t-kdom)) +1 -1) (acos (/ (vector3-x t-kdom) (* fcen ng)))) 0))
(print "tran: (even-y), " nm ", " (rad->deg t-angle) ", " Tmode "\n")
(set! Tsum (+ Tsum Tmode))))))
(arith-sequence 0 1 nm-t))
(set! res (get-eigenmode-coefficients tran-flux (arith-sequence 1 1 nm-t) #:eig-parity (+ eparity ODD-Y)))
(set! coeffs (list-ref res 0))
(set! kdom (list-ref res 3))
(map (lambda (nm)
(let ((t-kdom (list-ref kdom nm))
(Tmode (/ (sqr (magnitude (array-ref coeffs nm 0 0))) (list-ref input-flux 0))))
(if (> (vector3-x t-kdom) kdom-tol)
(begin
(set! t-angle (if (> (modulo-float (vector3-x t-kdom) (* fcen ng)) angle-tol)
(* (if (positive? (vector3-y t-kdom)) +1 -1) (acos (/ (vector3-x t-kdom) (* fcen ng)))) 0))
(print "tran: (odd-y), " nm ", " (rad->deg t-angle) ", " Tmode "\n")
(set! Tsum (+ Tsum Tmode))))))
(arith-sequence 0 1 nm-t)))
(let
((nm-r (- (floor (* (- fcen (vector3-y k)) d)) (ceiling (* (- (- fcen) (vector3-y k)) d))))
(nm-t (- (floor (* (- (* fcen ng) (vector3-y k)) d)) (ceiling (* (- (- (* fcen ng)) (vector3-y k)) d)))))
(set! res (get-eigenmode-coefficients refl-flux (arith-sequence 1 1 nm-r) #:eig-parity eparity))
(set! coeffs (list-ref res 0))
(set! kdom (list-ref res 3))
(map (lambda (nm)
(let ((r-kdom (list-ref kdom nm))
(Rmode (/ (sqr (magnitude (array-ref coeffs nm 0 1))) (list-ref input-flux 0))))
(if (> (vector3-x r-kdom) kdom-tol)
(begin
(set! r-angle (if (> (modulo-float (vector3-x r-kdom) fcen) angle-tol)
(* (if (positive? (vector3-y r-kdom)) +1 -1) (acos (/ (vector3-x r-kdom) fcen))) 0))
(print "refl:, " nm ", " (rad->deg r-angle) ", " Rmode "\n")
(set! Rsum (+ Rsum Rmode))))))
(arith-sequence 0 1 nm-r))
(set! res (get-eigenmode-coefficients tran-flux (arith-sequence 1 1 nm-t) #:eig-parity eparity))
(set! coeffs (list-ref res 0))
(set! kdom (list-ref res 3))
(map (lambda (nm)
(let ((t-kdom (list-ref kdom nm))
(Tmode (/ (sqr (magnitude (array-ref coeffs nm 0 0))) (list-ref input-flux 0))))
(if (> (vector3-x t-kdom) kdom-tol)
(begin
(set! t-angle (if (> (modulo-float (vector3-x t-kdom) (* fcen ng)) angle-tol)
(* (if (positive? (vector3-y t-kdom)) +1 -1) (acos (/ (vector3-x t-kdom) (* fcen ng)))) 0))
(print "tran:, " nm ", " (rad->deg t-angle) ", " Tmode "\n")
(set! Tsum (+ Tsum Tmode))))))
(arith-sequence 0 1 nm-t))))
(print "total:, " Rsum ", " Tsum ", " (+ Rsum Tsum) "\n")
The following Bash script executes the grating BSDF simulation for both polarizations over the angular range of -45° to +45° in increments of 5°. The output of each run is piped to a file. The data for the total reflectance and transmittance is collected in separate files for each polarization.
#!/bin/bash
d=3.5
h=1.9
g=0.7
for t in `seq -45 5 45`; do
meep d=${d} h=${h} g=${g} src-angle=${t} src-pol=1 |tee grating_d${d}_h${h}_g${g}_Ez_theta${t}.out;
grep total: grating_d${d}_h${h}_g${g}_Ez_theta${t}.out |cut -d , -f2- >> grating_Ez_d${d}_h${h}_g${g}.dat;
meep d=${d} h=${h} g=${g} src-angle=${t} src-pol=2 |tee grating_d${d}_h${h}_g${g}_Ez_theta${t}.out;
grep total: grating_d${d}_h${h}_g${g}_Hz_theta${t}.out |cut -d , -f2- >> grating_Hz_d${d}_h${h}_g${g}.dat;
done
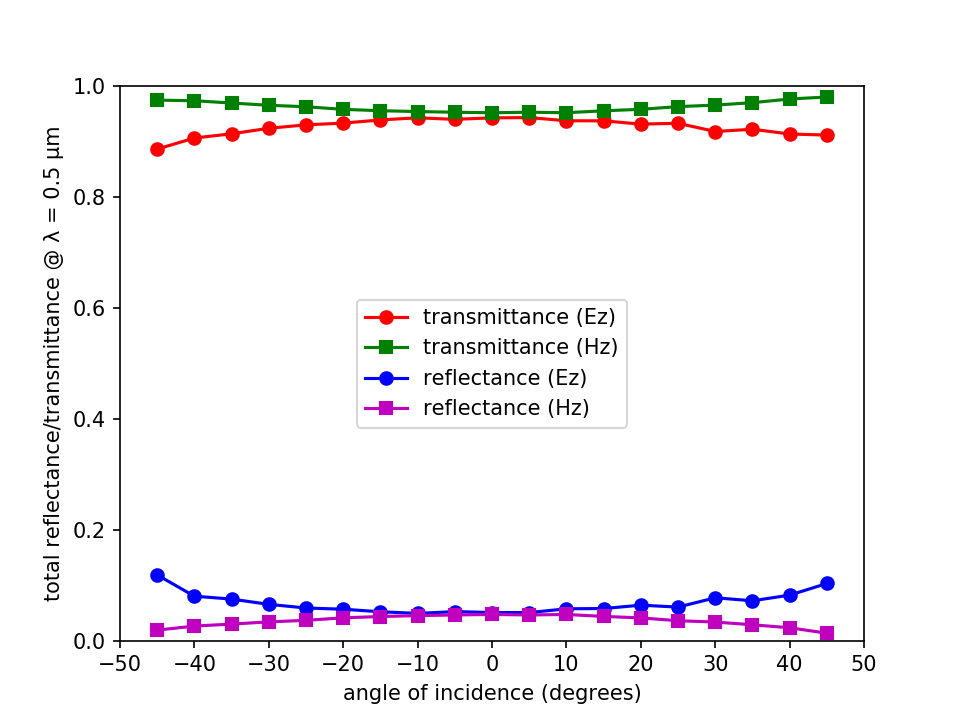
The Octave/Matlab script below plots the reflectance and transmittance spectra.
thetas = [-45:5:45];
ez_data = load('grating_Ez_d3.5_h1.9_g0.7.dat');
hz_data = load('grating_Hz_d3.5_h1.9_g0.7.dat');
plot(thetas,ez_data(:,2),'ro-');
hold on;
plot(thetas,hz_data(:,2),'gs-');
plot(thetas,ez_data(:,1),'bo-');
plot(thetas,hz_data(:,1),'ms-');
axis([-50 50 0 1]);
set(gca, 'xtick', [-50:10:50]);
set(gca, 'ytick', [0:0.2:1.0]);
legend("transmittance (Ez)","transmittance (Hz)","reflectance (Ez)","reflectance (Hz)");
xlabel("angle of incidence (degrees)");
ylabel("total reflectance/transmittance @ λ = 0.5 μm");
The following is the output for the reflected orders for an Ez-polarized source at an incident angle of +25°. The first numerical column is the diffraction order (an integer), the second is the angle of the mode (in degrees), and the third is the reflectance. The sign of the angles refers to the direction of rotation about the Z axis: clockwise (+) or counter-clockwise (-) with 0° along the -X direction.
0, -0.32, 0.00011259
1, 7.89, 0.00171405
2, -8.54, 0.00119997
3, 16.26, 0.00873309
4, -16.94, 0.00113014
5, 25.02, 0.03593260
6, -25.73, 0.00078624
7, 34.46, 0.00636958
8, -35.24, 0.00071590
9, 45.13, 0.00041392
10, -46.05, 0.00038857
11, 58.38, 0.00160692
12, -59.63, 0.00017113
Shown below is the output for the transmitted orders. Note that the fifth diffraction order at 14.27° has a transmittance of nearly 0.51. This indicates that 51% of the input power is directed into just a single mode. An application of this type of calculation for display applications would involve maximizing the reflectance or transmittance of a given diffraction order.
0, -0.19, 0.03480129
1, 4.59, 0.02409643
2, -4.96, 0.00130120
3, 9.39, 0.02907887
4, -9.78, 0.05293424
5, 14.27, 0.50628602
6, -14.66, 0.02359082
7, 19.25, 0.05468124
8, -19.65, 0.00661593
9, 24.39, 0.00175412
10, -24.81, 0.01615384
11, 29.75, 0.02172649
12, -30.18, 0.00517371
13, 35.41, 0.03408556
14, -35.88, 0.00400024
15, 41.51, 0.00015972
16, -42.01, 0.00049539
17, 48.24, 0.01024240
18, -48.81, 0.00154459
19, 56.02, 0.01787368
20, -56.70, 0.00272488
21, 65.85, 0.07193458
22, -66.79, 0.00265052
Finally, the plot below shows the total reflectance and transmittance (i.e., sum of all the diffraction orders) for both polarizations as a function of the angle of incidence of the planewave source. Due to the relatively low index of the grating, most of the input power is transmitted. Additionally, coherent scattering effects are weak which is why there is little variation in the results with the source angle and polarization. The intrinsic asymmetry of the grating design is verified by the asymmetry in the results for positive and negative angles.